http://www.hpfem.jku.at
START-Preis 2002
Herrn Dr. Joachim Schöberl wurde am 3. Juli 2002 der START-Preis 2002 von Frau Bundesministerin Gehrer in Wien überreicht. Foto
Der START-Preis ist mit 200.000 Euro pro Jahr für eine Dauer von sechs Jahren dotiert.
Details zum START-Programm (FWF)START Projekt "3D hp Finite Elemente: Schnelle Löser und Adaptivität"
Joachim Schöberl
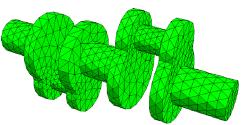
Mechanische Deformationen, magnetische Felder und viele weitere Problemstellungen aus Wissenschaft und Technik können mittels partiellen Differentialgleichungen mathematisch beschrieben werden. Die Finite Elemente Methode (FEM) ist die wohl leistungsfähigste Methode zur Computersimulation dieser Modelle. Dabei wird das zu berechnende Objekt in viele kleine Elemente wie Dreiecke, Tetraeder oder Quader zerlegt. Bild 1 zeigt ein Finite Elemente Netz einer Kurbelwelle. Diese Elemente werden verwendet, um Feldfunktionen wie eine mechanische Deformation, oder ein Magnetfeld näherungsweise darzustellen. Eine Möglichkeit ist es, in allen Eckpunkten der Elemente einen Funktionswert anzusetzen, und dazwischen linear zu interpolieren. Damit erhält man eine Beschreibung des Problems. Doch um die Lösung zu bestimmen, muß noch ein großdimensionales Gleichungssystem aufgelöst werden. Das Ergebnis, d.h. der Feldverlauf, kann dann graphisch dargestellt werden, und Kennzahlen können aus der Lösung extrahiert werden. Bild 2 zeigt die Verteilung der Materialspannungen in dieser Kurbelwelle.

Dank der sehr rasch wachsenden Rechenleistung heutiger Computer können immer kompliziertere Modelle immer genauer gelöst werden. Dabei kann man sagen, je größer das Problem wird, umso wichtiger sind effiziente Algorithmen. Bei der Finite Elemente Methode sind dabei vor allem zwei Aspekte entscheidend: Erstens, wie wird die Feinheit des Netzes gesteuert? In kritischen Bereichen müssen viele, kleinere Elemente verwendet werden, während in anderen Bereichen weniger, große Elemente ausreichend sind. Diese Netzsteuerung soll durch adaptive Algorithmen automatisch erfolgen. Der zweite wichtige Punkt ist der Gleichungslöser. Bei konventionellen Algorithmen wie beim Gauß'schen Eliminationsverfahren wächst die benötigte Rechenzeit überproportional mit der Problemgröße an. Moderne Verfahren hingegen arbeiten iterativ. Dabei wird durch gute Schätzverfahren die Lösung sukzessive verbessert. Damit kann ein proportionaler Zusammenhang von Problemgröße und benötigter Rechenzeit erreicht werden.
Eine Version der FEM ist die sogenannte h-Version. Hier wird die Genauigkeit durch die Anzahl der Elemente gesteuert. Der Spannungsverlauf in Bild 2 wurde z.B. unter Verwendung von 2 Millionen Unbekannten bestimmt. Eine andere Variante der FEM, die p-Version, arbeitet auf einem fixen Netz, und erhöht die Anzahl der Parameter pro Element. Der Vorteil dieser Methode ist, daß glatte Funktionen mit Polynomen höherer Ordnung sehr gut angenähert werden können. Lokale Effekte, wie z.B. die Spannungssingularitäten in den Kerben können wiederrum durch feinere Netze besser beschrieben werden. Die hp-Version verbindet nun beide Vorteile. Es werden sowohl die Netzfeinheit als auch der Polynomgrad variiert. Damit kann extrem (exponentiell) schnelle Konvergenz erreicht werden.
Mit dem aktuellen Stand der Forschung bei der hp-Version können zweidimensionale Probleme zufriedenstellend gelöst werden. Für dreidimensionale Probleme sind sowohl die automatische Netzsteuerung, als auch schnelle, iterative Gleichungslöser heiße Eisen in der Forschung. Der Projektleiter ist in der Theorie und in der praktischen Umsetzung der h-Version der FEM erfahren. Ziel dieses START Projektes ist es, wesentlich zur Theorie der hp-Version beizutragen, als auch die entsprechende Software zur Computersimulation von real-life Problemen zu entwickeln.

