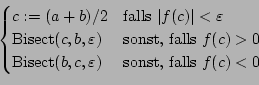
![[*]](crossref.png) ging es darum, die
Nullstelle von
f (x) : = sin(x) - x/2 im Intervall (a,b), mit
a = 0 und b = 1 zu bestimmen.
Unter der Voraussetzung
f (a) > 0 > f (b) kann dieses Problem
(für stetige Funktionen)
mittels Bisektion gelöst werden.
Der Bisektionsalgorithmus besteht für jedes Intervall [a, b]
im wesentlichen aus den Schritten
ging es darum, die
Nullstelle von
f (x) : = sin(x) - x/2 im Intervall (a,b), mit
a = 0 und b = 1 zu bestimmen.
Unter der Voraussetzung
f (a) > 0 > f (b) kann dieses Problem
(für stetige Funktionen)
mittels Bisektion gelöst werden.
Der Bisektionsalgorithmus besteht für jedes Intervall [a, b]
im wesentlichen aus den Schritten
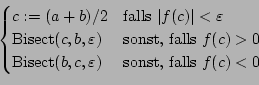
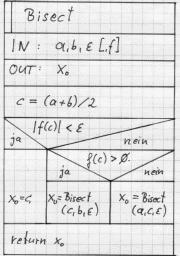
Dies ergibt die Funktionsdefinition für Bisect() welche
mit
x0 = Bisect(a,b,1e-6);
aufgerufen wird und zur Version 1 des Bisektionsprogrammes führt.
(siehe Bisect1.cc)
double Bisect1(const double a, const double b, const double eps)
{
double x0, fc, c = (a+b)/2;
fc = sin(c) - 0.5*c;
if ( fabs(fc) < eps )
{
x0 = c; // end of recursion
}
else if ( fc > 0.0 )
{
x0 = Bisect1(c,b,eps); // search in right intervall
}
else // i.e., fc < 0.0
{
x0 = Bisect1(a,c,eps); // search in left intervall
}
return x0; // return the solution
}
|
Um das Programm etwas flexibler zu gestalten, werden wir die fix
in Bisect1() einprogrammierte Funktion f (x) durch die
globale Funktion
double f(const double x) // declaration and
{ return sin(x) - 0.5*x ; } // definition of function f(x)
|
ersetzen.
Gleichzeitig könnten wir den Funktionsparameter eps durch eine globale
Konstante EPS ersetzen, sodaß sich Version 2 ergibt.
(siehe Bisect2.cc)
Die Flexibilität der Bisektionsfunktion läßt sich weiter erhöhen
indem wir die auszuwertende Funktion f (x) als Variable in der
Parameterliste übergeben. Eine Funktion als Parameter/Argument wird immer als
Zeiger übergeben, d.h., eine Funktion als Argument muß wie
die Deklaration für f6 auf Seite ![[*]](crossref.png) aufgebaut sein.
Konkret heißt dies:
aufgebaut sein.
Konkret heißt dies:
double (*func)(double) ist ein Zeiger auf eine
Funktion func mit einer double-Variablen als Argument
und double als Typ des Rückkehrwertes.
Dies erlaubt uns die Funktionsdeklaration und -definition von
Bisect3()
// declaration of Bisect3
double Bisect3(double (*func)(double), const double a,
const double b, const double eps=1e-6);
...
main()
{...}
// definition of Bisect3
double Bisect3(double (*func)(double), const double a,
const double b, const double eps)
{
double x0, fc, c = (a+b)/2;
fc = func(c); // calculate value of parameter function
if ( fabs(fc) < eps )
{
x0 = c; // end of recursion
}
else if ( fc > 0.0 )
{
x0 = Bisect3(func,c,b,eps); // search in right intervall
}
else // i.e., fc < 0.0
{
x0 = Bisect3(func,a,c,eps); // search in left intervall
}
return x0; // return the solution
}
|
Das vierte Argument (eps) in der Parameterliste von Bisect3()
ist ein optionales Argument, welches
beim Funktionsaufruf nicht übergeben werden muß. In diesem Fall
wird diesem optionalen Argument sein, in der Funktionsdeklaration festgelegter,
Standardwert automatisch zugewiesen. In unserem Falle würde also der Aufruf
im Hauptprogramm
x0 = Bisect3(f,a,b,1e-12)
die Rekursion bei
| f (c)| < ![]() : = 10-12 abbrechen,
während
: = 10-12 abbrechen,
während
x0 = Bisect3(f,a,b)
schon bei
| f (c)| < ![]() : = 10-6 stoppt.
(siehe Bisect3.cc)
: = 10-6 stoppt.
(siehe Bisect3.cc)
Wir könnten jetzt eine weitere Funktion
// declaration and
double g(const double x)
// definition of function g(x)
{ return -(x-1.234567)*(x+0.987654) ; }
|
deklarieren und definieren, und den Bisektionsalgorithmus
in Version 3.
(siehe Bisect3.cc)
mit ihr aufrufen:
x0 = Bisect3(g,a,b,1e-12)
Bemerkung:
Da wir unsere als Argument in Bisect3
übergebene Funktion func ein reiner INPUT-Parameter ist,
sollten wir sie noch mit const kennzeichnen.
Allerdings ist die richtige Kennzeichnung des ersten Arguments in Bisect3
double Bisect3(double (* const func)(double), const double a,
const double b, const double eps=1e-6);
|
am Anfang etwas verwirrend.
Unser Programm
arbeitet zufriedenstellend für
f (x) = sin(x) - x/2
und liefert für die Eingabeparameter a = 1 und b = 2 die richtige Lösung
x0 = 1.89549, desgleichen für a = 0 und b = 2
allerdings wird hier bereits die (triviale) Lösung x0 = 0 nicht gefunden,
da a = 0 eingegeben wurde. Bei den Eingaben
a = 0, b = 1 bzw. a = - 1, b = 0.1 (
x0 : = 0 ![]() [a, b]) bricht das Programm
nach einiger Zeit mit
Segmentation fault
ab, da die Rekursion nicht
abbricht und irgendwann der für Funktionsaufrufe reservierte Speicher
(Stack) nicht mehr ausreicht.
[a, b]) bricht das Programm
nach einiger Zeit mit
Segmentation fault
ab, da die Rekursion nicht
abbricht und irgendwann der für Funktionsaufrufe reservierte Speicher
(Stack) nicht mehr ausreicht.
Können wir unser Programm so absichern, daß z.B. die vorhandene Nullstelle x0 = 0 sowohl in [0, 1] als in [- 1, 0.1] gefunden wird? Welche Fälle können bzgl. der Funktionswerte f (a) und f (b) auftreten (vorläufige Annahme: a < b)?
Bisect3().
Diese Fallunterscheidung führt uns zum folgenden Struktogramm und zur Version 4. (siehe Bisect4.cc)
Struktogramm:
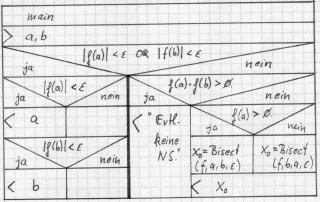
Als krönenden Abschluß definieren wir uns im Programm weitere Funktionen
h(x) = 3 - ex,
t(x) = 1 - x2, fragen den Nutzer welche math. Funktion
für die Nullstellensuche benutzt werden soll und berechnen
die Nullstelle(n) im gegebenen Intervall.
Diese Auswahl kann leicht mit einer switch-Anweisung realisiert werden und
führt zu Version 5 des Programmes.
(siehe Bisect5.cc)
Bemerkung:
Die drei Funktionen Bisect[1-3]() unterscheiden sich in ihren
Parameterlisten. Deshalb können alle drei Funktionen unter dem Namen
Bisect() verwendet werden, da sich ihre Signaturen unterscheiden
und somit der Compiler genau weiß, welche Funktion Bisect()
verwendet werden soll.
(siehe Bisect6.cc)