4.6 Nichtabweisender Zyklus (do-while-Schleife)

Beim nichtabweisenden Zyklus steht die Anzahl der Durchläufe nicht a-priori fest, der Abbruchtest erfolgt nach dem Durchlauf eines Zyklus. Somit durchläuft der nichtabweisende Zyklus mindestens einmal die Anweisungen im Zyklusinneren.

Die allgemeine Form ist

do 
  <anweisung>
while (<logischer ausdruck>) ;

Struktogramm:

Beispiel: Es wird solange ein Zeichen von der Tastatur eingelesen, bis ein x eingegeben wird. (siehe Ex460.cc)

//	Example : Input of a character until 'x' 
#include <iostream.h>
main()
{
 char ch;
 
 do
   {
     cout << endl << "Input command (x = exit, ...)  ";
     cin  >> ch;
   }
 while ( ch != 'x' );
 
 cout << endl << "          Exit program" 
      << endl << endl;
}

Betrachten wir ein etwas anspruchsvolleres Beispiel, und zwar soll die Lösung von sin(x) = x/2 mit x $\in$ (0,$\pi$) bestimmt werden. Hierzu betrachtet man die äquivalente Nullstellenaufgabe: Bestimme die Nullstelle x₀ $\in$ (0,$\pi$) der Funktion f (x) : = sin(x) - x/2 = 0 .
Analytisch: Kein praktikabler Lösungsweg vorhanden.
Graphisch: Die Funktion f (x) wir graphisch dargestellt und das Lösungsintervall manuell verkleinert (halbiert). Diesen Prozeß setzt man so lange fort, bis x₀ genau genug, d.h., auf eine vorbestimmte Anzahl von Stellen genau, bestimmt werden kann.



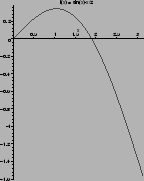
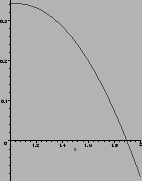
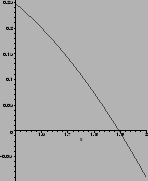
Numerisch: Obiges, graphisches Verfahren kann auf ein rein numerisches Verfahren im Computer übertragen werden (der MAPLE-Aufruf fsolve(sin(x)=x/2,x=0.1..3 liefert als Näherungsergebnis x₀ = 1.895494267 ). (siehe Ex462.mws) Wir entwickeln ein Programm zur Bestimmung der Nullstelle von f (x) : = sin(x) - x/2 im Intervall [a, b] mittels Intervallhalbierung, wobei zur Vereinfachung angenommen wird, daß f (a) > 0 und f (b) < 0 ist. Der Mittelpunkt des Intervalls sei mit c : = (a + b)/2 bezeichnet. Dann können wir über die Lösung folgendes aussagen: $$\begin{cases}x_0 := c & \text{falls } f(c) = 0 \\ x_0 \i... ...c) > 0 \\ x_0 \in [a,c] & \text{falls } f(c) < 0 \end{cases}$$ . Durch Redefinition der Intervallgrenzen a und b kann die Nullstellensuche auf das kleinere (halbierte) Intervall reduziert werden. Wir demonstrieren die Umsetzung mittels eines nichtabweisenden Zyklus. (siehe Ex462.cc)

Struktogramm:

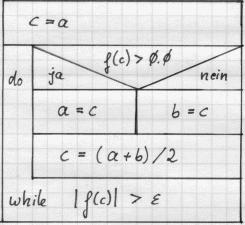
Obige Bisektion kann auch mittels eines abweisenden Zyklus realisiert werden.

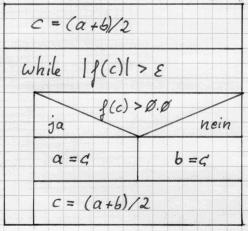
//   Nullstellenberechnung durch Bisektion in [a,b]
#include <iostream.h>
#include <math.h>

main()
{
 const double Eps = 1e-6;
 double a,b,c,fc;
 
 ...
 cin >> a; cin >> b;
//      Check that f(a) > 0,  f(b) < 0 !! 
 ...
//              Do-While loop
  c  = a;             // since f(a) > 0
  fc = sin(c)-c/2;
  do 
   {
    if ( fc > 0.0 )
     {
       a = c;
     }
    else
     {
       b = c;
     }
    c  = (a+b)/2.0;
    fc = sin(c)-c/2;
   }
  while ( fabs(fc) > Eps);
//  while ( fabs(fc) != 0.0);   // endless!! Why ?

  cout << " Nullstelle = " << c << endl;
}

Da Gleitkommazahlen nur mit limitierter Genauigkeit arbeiten resultiert ein Abbruchtest f (c) = 0 meist in einem endlosen Programm. Dem ist ein Abbruchtest wie | f (c)| < $\varepsilon$ mit einer vorgegebenen Genauigkeit 0 < $\varepsilon$ $\ll$ 1 vorzuziehen.

Bemerkung: Zählzyklen (for), welche mindestens einen Zyklus ausführen, können sowohl durch abweisende (while) als auch durch nichtabweisende Zyklen (do while) äquivalent ausgedrückt werden. Diese Äquivalenz kann bei Verwendung der Anweisungen in § 4.8 verloren gehen. Falls in einem Zählzyklus der Abbruchtest stets FALSE ergibt, d.h. der Schleifenkörper wird nie ausgeführt, dann ist der entsprechende abweisende Zyklus nach wie vor äquivalent. Jedoch ist der nichtabweisende Zyklus nicht mehr äquivalent, da der dortige Schleifenkörper auch in diesem Fall einmal abgearbeitet wird. (siehe Loops.cc) Siehe das Beispielfile Loops.cc.