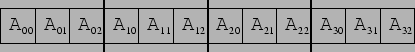



Nächste Seite: 5.2 Strukturen
Aufwärts: 5.1 Felder
Vorherige Seite: 5.1.1 Eindimensionale Felder
Inhalt
Index
5.1.2 Mehrdimensionale Felder
Die Einträge der bisher betrachteten 1D-Felder sind im
Speicher hintereinander gespeichert (Modell des linearen Speichers), z.B,
wird der Zeilenvektor
als
double x[5];
vereinbart und gespeichert als
wobei jede Zelle 8 Byte lang ist.
Ein zweidimensionales (statisches) Feld, z.B., eine Matrix A mit N = 4 Zeilen
und M = 3 Spalten
AN x M : =

kann im Speicher ebenfalls nur linear gespeichert werden, d.h.,
Daraus ergeben sich zwei Möglichkeiten der 2D-Feldvereinbarung:
- Variante 1 : Als 2D-Array.
double A[N][M]; // Declaration
A[3][1] = 5.0; // Initialize A(3,1)
|
- Variante 2 : Als 1D-Array.
double A[N*M]; // Declaration
A[3*M+1] = 5.0; // Initialize A(3,1)
|
Beispiel: Als Beispiel betrachten wir die Multiplikation
der Matrix
AN x M
bestehend aus N = 4 Zeilen und M = 3 Spalten
mit einem Zeilenvektor
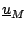 der Länge M.
Das Ergebnis ist ein Zeilenvektor
der Länge M.
Das Ergebnis ist ein Zeilenvektor
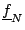 der Länge N,
d.h.,
der Länge N,
d.h.,
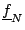 : = AN x M .
: = AN x M . 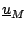 .
Die Komponenten von
.
Die Komponenten von
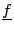 = [f0, f1,..., fN-1]T
berechnen sich zu
(siehe Ex514.cc)
= [f0, f1,..., fN-1]T
berechnen sich zu
(siehe Ex514.cc)
fi : =
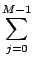 Ai, j . uj
Ai, j . uj 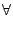 i
i = 0,...,
N - 1 .
Höherdimensionale Felder können analog zu Version 1 deklariert und benutzt
werden. In Variante 2 muß auf ein Element B(i, j, k) eines dreidimensionalen
Feldes double B[L,N,M]; mittels B[i*M*N+j*M+k] zugegriffen
werden.




Nächste Seite: 5.2 Strukturen
Aufwärts: 5.1 Felder
Vorherige Seite: 5.1.1 Eindimensionale Felder
Inhalt
Index
Gundolf Haase
2004-01-15