4.4 Der Zählzyklus (for-Schleife)

Beim Zählzyklus steht die Anzahl der Zyklendurchläufe a-priori fest, der Abbruchtest erfolgt vor dem Durchlauf eines Zyklus. Die allgemeine Form ist

for (<ausdruck_1>; <ausdruck_2>; <ausdruck_3>) 
  <anweisung>

Am besten sei der Zählzyklus an einem Beipiel erläutert.

Beispiel: Es ist die Summe der ersten 5 natürlichen Zahlen zu berechnen. (siehe Ex440.cc)

//				Example : sum of natural numbers
#include <iostream.h>

main()
{
 int i,isum,n;                   // loop index, sum, last index
 
 n = 5;                          // initialize last index
 
 isum = 0;                       // initialize sum (integer !)
 for ( i = 1; i <= n; i=i+1)
   {
     isum = isum + i;
   }
 cout << endl << "Sum of first " << n 
      << " natural numbers = " << isum << endl; 
}

Im obigen Programmbeispiel ist i die Laufvariable des Zählzyklus, welche mit i = 1 (<ausdruck_1>) initialisiert, mit i = i+1 (<ausdruck_3>) weitergezählt und in i <= n (<ausdruck_2>) bzgl. der oberen Grenze der Schleifendurchläufe getestet wird. Im Schleifeninneren sum = sum + i; (anweisung) erfolgen die eigentlichen Berechnungsschritte des Zyklus. Die Summationsvariable sum muß vor dem Eintritt in den Zyklus initialisiert werden.

Eine kompakte Version dieser Summationsschleife (korrekt, aber sehr schlecht lesbar) wäre :
for (isum = 0, i = 1; i <= n; isum += i, i++)
Man unterscheide dabei zwischen dem Abschluß einer Anweisung ``;'' und dem Trennzeichen ``,'' in einer Liste von Ausdrücken. Diese Listen werden von links nach rechts abgearbeitet.

Der <ausdruck_2> ist stets ein logischer Ausdruck (§ 3.3-3.4) und <ausdruck_3> ist ein arithmetischer Ausdruck zur Manipulation der Laufvariablen, z.B.

 i++
 j = j-2
 j += 2
 x = x+h         // float-Typ
 k = 2*k         // Verdoppelung
 l = l/4         // Viertelung - Vorsicht bei Integer

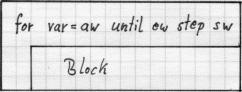
Struktogramm:

• Die Laufvariable kann eine einfache Variable aus § 2.1 sein, z.B., int oder double .
• Vorsicht bei Verwendung von Gleitkommazahlen (float, double) als Laufvariable. Dort ist der korrekte Abbruchtest wegen der internen Zahldarstellung u.U. nicht einfach zu realisieren. (siehe Loop_Float.cc)

Beispiel: Es sei die Doppelsumme

sum = $$\sum_{{k=1}}^{n}$$$$\underbrace{{\sum_{i=1}^k \frac{1}{i^2}}}_{{t_k}}^{}\,$$ = $$\sum_{{k=1}}^{n}$$t_k

für einzugebende n zu berechnen.

(siehe Ex442.cc)

Struktogramm:

 
//			Example: double sum
#include <iostream.h>
main()
{
 int    i,k,n;                  // loop index, sum, last index
 double sum_i,sum_k;            // outer and inner sum
 
 cout << "  Input n : "; cin  >> n;     // read n

 sum_k = 0.0;                           // initialize outer sum
 
 for ( k = 1; k <= n; k++)
  {
    sum_i = 0.0;                        // initialize inner sum
    for ( i = 1; i <= k; i++)           // last index depends on k !!
     {
        sum_i = sum_i + 1.0/i/i;
     }
    cout << "  Sum (" << k << ") = " << sum_i << endl;
    sum_k = sum_k + sum_i;              // sum_k grows unbounded
  }
 cout << "  Double-Sum (" << n << ") = " << sum_k << endl; 
}

Weitere einfache Beispiele berechnen die Summe der ersten geraden natürlichen Zahlen (siehe Ex443.cc) und das Zählen eines CountDowns. (siehe Ex444.cc)

Die folgenden Beispiele verdeutlichen die Problematik der begrenzten Genauigkeit von Gleitkommazahlen in Verbindung mit Zyklen und einige Tips zu deren Umgehung.

Beispiel: Ausgabe der diskreten Knoten x_i des Intervalls [0, 1], welches in n gleichgroße Teilintervalle zerlegt wird, d.h., (siehe Loop_Float.cc)

x_i = i ^. h    ,  i = 0,..., n        mith = $${\frac{{1-0}}{{n}}}$$

Struktogramm:

 
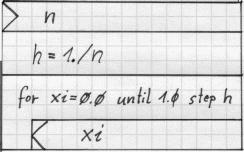
main()
{
 float xa,xe,xi,h;
 int   n;
 
 cin  >> n;          // # subintervals 
 xa = 0.0e0;         // # start interval
 xe = 1.0e0;         // # end interval
 h   = (xe-xa)/n;    // length subinterval

 for (xi = xa; xi <= xe; xi += h)
   {
    cout << xi << endl;
   }
}

Da Gleitkommazahlen nur eine limitierte Anzahl gültiger Ziffern besitzen, kann es (meistens) passieren, daß der letzte Knoten x_n nicht ausgegeben wird. Nur für n = 2^k  , k $\in$ $\mathbb {N}$ kann in unserem Beispiel eine korrekte Abarbeitung des Zählzyklus garantiert werden. Auswege sind

1. Änderung des Abbruchtests in xi <= xe + h/2.0 , jedoch ist x_n immer noch fehlerbehaftet.

    
    for (xi = xa; xi <= xe + h/2.0; xi += h)
      {
       cout << xi << endl;
      }
   

2. Zyklus mit int-Laufvariable

    
    for (i = 0; i <= n; i++)
      {
       xi = xa + i*h;
       cout << xi << endl;
      }
   

Die gemeinsame Summation kleinerer und größerer Zahlen kann ebenfalls zu Ungenauigkeiten führen. Im Beispiel wird die Summe s1 : = $\sum\limits_{{i=1}}^{{n}}$1/i² mit der (theoretisch identischen) Summe s2 : = $\sum\limits_{{i=n}}^{{1}}$1/i² für große n (65.000, 650.000) verglichen. (siehe Reihe.cc)

#include <iostream.h>
#include <math.h>
#include <float.h>

main()
{
 float s1,s2;
 int i,n ;

 cout << "The first sum will be rather precise until  n = "
     << ceil(sqrt(1./FLT_EPSILON)) << endl;
 cin >> n;
 
 s1 = 0.0; 
 for (i=1; i<=n; i++)
   {
     s1 += 1.0/i/i;
   }
 cout << s1 << endl;
 
 s2 = 0.0; 
 for (i=n; i>=1; i--)
   {
     s2 += 1.0/i/i;
//   s2 += 1.0/(i*i);     results in inf
//                        since i*i is longer than int supports
   }
 cout << s2 << endl;
 cout << s2-s1 << endl;
}

Das numerische Resultat in s2 ist genauer, da dort zuerst alle kleinen Zahlen addiert werden, welche bei s1 wegen der beschränkten Anzahl gültiger Ziffern keinen Beitrag zur Summation mehr liefern können. Gleichzeitig ist zu beachten, daß die Berechnung von 1.0/(i*i) in einem Überlauf endet, da i*i nicht mehr in int-Zahlen darstellbar ist. Dagegen erfolgt die Berechnung von 1.0/i/i vollständig im Bereich der Gleitkommazahlen.